The results of evaluating the correlation between the density and compressive strength of Portland cement at the age of 28 days with different values of the water-cement ratio (W/C = 0.3, 0.4, and 0.5) are presented. Correlation dependencies are determined using linear coefficients of Pearson, Spearman and Kendall. It is shown that with an increase in the water-cement ratio, the correlation between the density and compressive strength becomes stronger. It was also found that the most corre-lated experimental data (W/C = 0.5) can be considered dependent random variables. Through information criteria AIC and BIC, Clayton's copula was selected for this experimental data. Use the copula allows generating the required number of test results of dependent random variables in probabilistic modeling.
Portland cement, strength, density, correlation coefficients, dependent random variables, copula
Введение. Прочность на сжатие и средняя плотность затвердевшего портландцемента занимают одно из важных мест среди его физико-механических свойств. С точки зрения математической статистики прочность и плотность являются случайными величинами. Формирование закона распределения для случайных величин, характеризующих свойства материалов на основе портландцемента, может происходить под влиянием различных факторов, таких как, рецептурные и технологические отклонения при изготовлении материалов, строение и дефектность материалов, процесс получения экспериментальных данных. Например, чаще всего прочность на сжатие тяжелого бетона можно описать нормальным законом распределения [1], но также встречаются и другие законы распределения, например, распределение Вейбулла [2].
В теории вероятностей различают независимые и зависимые случайные величины. Независимые случайные величины – это такие случайные величины, у которых совместную плотность распределения можно представить через произведение их отдельных плотностей распределения. При этом значение одной независимой случайной величины, при её генерации, не влияет на значения остальных случайных величин. У зависимых случайных величин присутствует связь между ними, то есть значение одной случайной величины влияет на значения других случайных величин из рассматриваемой совокупности. Наличия зависимости или независимости между случайными величинами важно для корректного моделирования вероятностными методами. Одним из способов оценки вероятностной зависимости между случайными величинами – это применение различных корреляционных линейных и ранговых коэффициентов. Коэффициенты корреляции часто применяют для анализа свойств строительных материалов, так для древесины присутствует положительная корреляционная зависимость между её плотностью и её прочностью на сжатие вдоль волокон, и отрицательная корреляционная зависимость между относительной влажностью древесины и её модулем упругости [3].
При моделировании с помощью методов теории вероятностей, например, вероятностная оптимизация [4, 5], возникает потребность применения совместных распределений нескольких случайных величин. При этом может возникать трудность в генерации зависимых случайных величин. Одним из методов для корректной генерации зависимых случайных величин является применение копул.
В данной работе представлена оценка корреляционной зависимости межу средней плотностью и прочностью на сжатие для затвердевшего портландцемента. Оценка производится для составов с различными величинами водоцементного отношения (В/Ц = 0,3; 0,4 и 0,5) с помощью коэффициентов Пирсона, Спирмена и Кендалла. Для состава с наиболее коррелированными экспериментальными данными выполняется построение копулы.
Методы и материалы.
Для испытаний применялся портландцемент марки ЦЕМ I 42.5 Н и дистиллированная вода. Рентгенофазовый анализ негидратированного портландцемента показал следующий фазовый состав: C3S – 57%, C2S – 23%, C3A – 5%, C4AF – 11%, Ca2SO4 – 3%. В эксперименте было рассмотрены три величины водоцементного отношения для цементной пасты: В/Ц = 0,3; 0,4 и 0,5. Образцы для испытаний изготавливались в виде кубов с размерами 2х2х2 см3. Твердение образцов осуществлялось в воде при нормальных условиях в течение 28 суток согласно ГОСТ 30744-2001 «Цементы. Методы испытаний с использованием полифракционного песка». В 28 сутки образцы подвергались испытаниям на прочность при сжатии, непосредственно перед испытаниями образцы доставались из ванны с водой и протирались влажной тряпкой для удаления капель воды, затем проводились геометрические замеры образцов и их взвешивание. Количество образцов для проведения испытаний принималось 100 шт. для каждого вида исследуемых составов. Такое количество образцов для испытаний принято из-за проблемы «проклятие размерности» (curse of dimensionality) [6].
Оценка корреляционной зависимости между средней плотностью и прочностью на сжатие затвердевшего портландцемента выполнялась с помощью линейного коэффициента Пирсона [7] и линейных ранговых коэффициентов Спирмена и Кендалла [8, 9]. Также проверялись гипотезы о принадлежности нормальному закону распределения для всех экспериментальных данных с помощью критерия Шапиро-Уилка [10].
Линейный коэффициент Пирсона применяется для оценки корреляции между случайными величинами подвергнутых нормальному закону распределению, что подходит для таких случайных величин как плотность и прочность на сжатие материалов на основе портландцемента. Вычисление коэффициента корреляции по Пирсону для двух случайных величин x и y выполняется по формуле 1:
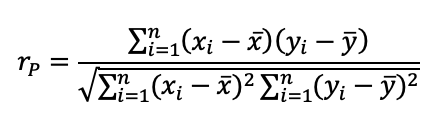(1)
Значение коэффициента корреляции Пирсона лежит на отрезке [-1;1]. Значение 1 означает прямую корреляцию, -1 – означает обратную корреляцию, а значение 0 указывает на отсутствие корреляционной зависимости.
Коэффициент корреляции Спирмена также оценивает линейную связь между случайными величинами, но корреляция является ранговой, т.е. при вычислениях используют не числовые значения случайной величины, а соответствующие им ранги:
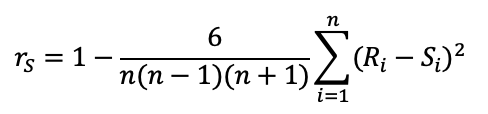(2)
где: Ri – ранг наблюдения xi в ряду x;
Si – ранг наблюдения yi в ряду y.
Коэффициент Кендалла также является линейным ранговым коэффициентом корреляции и вычисляется по следующей формуле:
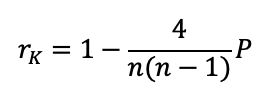(3)
где: P – количество инверсий, образованных величинами yi, расположенными в порядке возрастания соответствующих xi.
Величины ранговых коэффициентов Спирмена и Кендалла, также, как и коэффициент Пирсона, принадлежат [-1;1].
Недостатком линейных коэффициентов корреляции Пирсона, Спирмена и Кендалла является то, что с помощью них невозможно выполнить оценку нелинейной корреляционной зависимости, которая также может присутствовать между случайными величинами. В свою очередь это означает, что невозможно с помощью них достоверно утверждать об отсутствии зависимости между случайными величинами при отсутствии корреляционной зависимости (коэффициент корреляции →0). Но при стремлении показателя линейного коэффициента корреляции к 1.0 можно достоверно утверждать о наличии зависимости между случайными величинами.
Формирование совместных функций распределения для зависимых случайных величин можно осуществить с помощью копул, особенно данный метод хорошо подходит к распределениям с тяжелыми хвостами. Копула – многомерная функция распределения с областью определения [0,1]n. Все маргинальные распределения случайных величин, формирующие копулу, равномерны на интервале [0,1]. Обоснование получения копул объясняется теоремой Склара [11]. На сегодняшний день копулы применяют в экономических науках [12, 13], метеорологических науках [14, 15], в инженерных науках, в том числе связанных с расчетами искусственных сооружений [16, 17].
Различают разные классы копул, а именно, эллиптические копулы и архимедовы копулы. К первому относятся нормальная (гауссова) копула, t-копула (копула Стьюдента) и др., ко второму относятся такие копулы как копула Клейтона, копула Гумбеля, копула Франка и др. При анализе экспериментальных данных для получения их копулы наиболее подходящими являются ранговые коэффициенты корреляции Спирмена и Кендалла, так как могут присутствовать распределения с тяжелыми хвостами [18]. Выбор копулы можно выполнить c помощью информационного критерия Акаике (AIC) [19] и байесовского информационного критерия (BIC) [20].
(4)
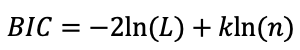(5)
где: L – максимизированное значение функции правдободобия,
k – количество параметров копулы,
n – количество экспериментальных данных.
Результаты исследования
Проверка гипотезы о принадлежности нормальному закону распределения для всех экспериментальных данных с помощью критерия Шапиро-Уилка для α = 0,05 показала, что нулевая гипотеза (H0: случайная величина подчиняется нормальному закону распределения) отклоняется.
Вычисленные коэффициенты корреляции по формулам 1, 2 и 3 между средней плотностью и прочностью на сжатие для различных составов приведены в табл. 1.
Таблица 1 – Коэффициенты корреляции для различных величин В/Ц в портландцементе
|
В/Ц |
Количество испытаний, шт. |
Коэффициент Пирсона, rP |
Коэффициент Спирмена, rS |
Коэффициент Кендалла, rK |
|
0,3 |
100 |
0,00 |
0,07 |
0,05 |
|
0,4 |
100 |
0,26 |
0,22 |
0,14 |
|
0,5 |
100 |
0,41 |
0,41 |
0,28 |
Результаты в таблице 1 показывают, что увеличение водоцементного отношения ведет к увеличению показателей коэффициентов корреляции, то есть корреляция между средней плотностью и прочностью на сжатие становится сильнее для составов с большим содержанием воды.
На рисунках 1-3 представлены графики поля экспериментальных точек, на которых также указаны гистограммы маргинальных случайных величин (средняя плотность P, г/см3, и прочность на сжатие R, МПа) и восстановленные с помощью ядерного сглаживания их плотности распределения [21, 22].
Из рисунков 1-3 также видно, что наибольшей корреляционной зависимостью обладает состав с В/Ц=0,5. Несмотря на то, что критерий Шапиро-Уилка отклонил гипотезу о нормальном законе распределения экспериментальных данных, в таблице 2 приводится информация о величинах среднего значения прочности на сжатие и величинах среднего значения средней плотности, и коэффициенты вариации.
Для состава с наибольшими корреляционными коэффициентами (В/Ц=0,5) выбор копулы с помощью информационных критериев AIC и BIC показал, что наиболее подходящей копулой является копула Клейтона с θ=0.8. Копула Клейтона относится к классу архимедовых копул с генератором (t)=(t-θ-1)/θ, где θ ∊ [-1,+
]\{0}Двумерная копула Клейтона вычисляется по формуле 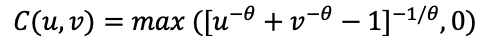6:
(6)
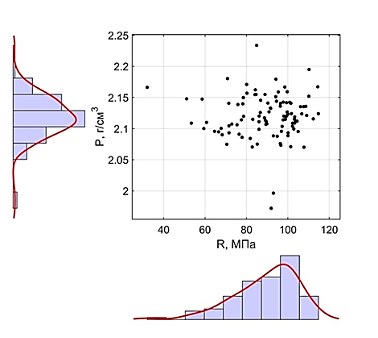Рисунок 1 – Поле экспериментальных точек и гистограммы маргинальных случайных величин с восстановленными плотностями распределения для состава с В/Ц=0,3
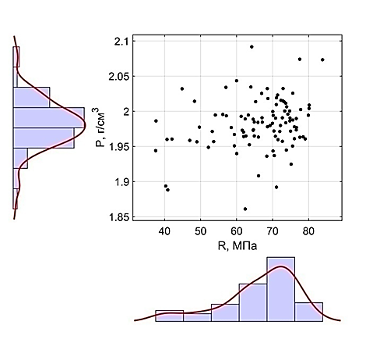Рисунок 2 – Поле экспериментальных точек и гистограммы маргинальных случайных величин с восстановленными плотностями распределения для состава с В/Ц=0,4
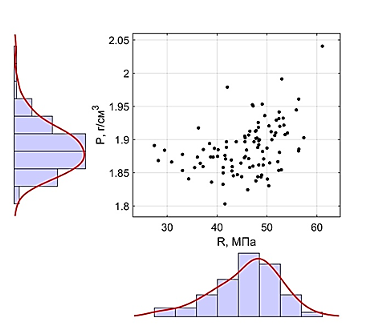Рисунок 3 – Поле экспериментальных точек и гистограммы маргинальных случайных величин с восстановленными плотностями распределения для состава с В/Ц=0,5
Функция плотности распределения для подобранной копулы Клейтона изображена на рисунке 4. Генерация 500 точек для средней плотности P и прочности на сжатие R портландцемента с помощью копулы Клейтона изображена на рисунке 5. Коэффициенты корреляции для данной генерации показали следующие значения: rP=0.44; rS=0.40; rK =0.28.
Таблица 2 – Средние значения и коэффициенты вариации экспериментальных данных для различных В/Ц портландцемента
|
В/Ц |
Среднее значение прочности на сжатие, МПа |
Коэффициент вариации прочности на сжатие, % |
Среднее значение средней плотности, г/см3 |
Коэффициент вариации средней плотности, % |
|
0,3 |
89,6 |
17,1 |
2,120 |
1,7 |
|
0,4 |
66,2 |
15,9 |
1,982 |
1,9 |
|
0,5 |
45,9 |
14,6 |
1,888 |
2,0 |
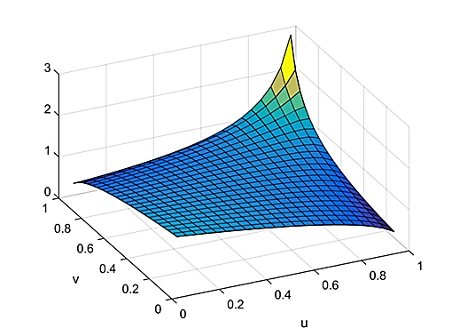Рисунок 4 – Функция плотности распределения (pdf) копулы Клейтона
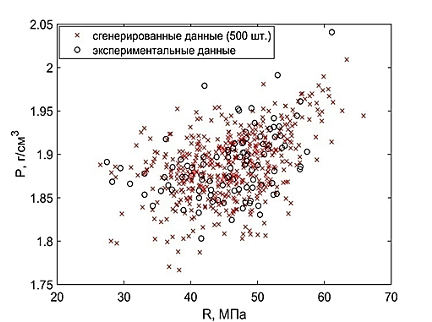Рисунок 5 – Генерация 500 точек с помощью копулы Клейтона для R и P
Выводы.
Проведены эксперименты по определению средней плотности и прочности на сжатие для портландцемента в возрасте 28 суток с разными величинами водоцементного отношения (В/Ц=0.3, 0.4 и 0.5).
Вычислены линейные коэффициенты корреляции (Пирсона, Спирмена и Кендалла) между средней плотностью и прочностью на сжатие затвердевшего портландцемента с различными величинами В/Ц. Вычисления показали, что с увеличением содержания воды повышается корреляция между средней плотностью и средней прочностью на сжатие.
Для состава с В/Ц=0,5, состав с наибольшей корреляционной зависимостью, среднюю плотность и прочность на сжатие можно считать зависимыми случайными величинами. Для этих случайных величин выбрана копула Клейтона. С помощью копулы можно генерировать необходимое число результатов испытаний зависимых случайных величин, что необходимо при вероятностном моделировании.
1. Osipov S.N. Ob ocenke nadezhnosti rezul'tatov ispyta-niy fizicheskih svoystv stroitel'nyh materialov // Nauka i tehnika. – 2014. – №. 5. – S. 18–24.
2. Aït-Mokhtar A., Belarbi R., Benboudjema F., Burlion N., Capra B., Carcassès M., Colliat J.-B., Cussigh F., Deby F., Jacquemot F., de Larrard T., Lataste J.-F., Bescop L., Pierre M., Poyet S., Rougeau P., Rougelot T., Sellier A., Séménadisse J., Torrenti J.-M., Trabelsi A., Turcry P., Yanez-Godoy H. Experi-mental Investigation of the Variability of Concrete Durability Properties // Cement and Concrete Research. – 2013. – Vol. 45. – P. 21–36.
3. Chirkov V.P. Prikladnye metody teorii nadezhnosti v raschetah stroitel'nyh konstrukciy. Uchebnoe posobie dlya vuzov zh.-d. transporta. – M.: Marshrut, 2006. – 620 s.
4. Thanedar P. B., Kodiyalam S. Structural Optimization Us-ing Probabilistic Constraints // Structural optimization. – 1992. – Vol. 4, № 3-4. – P. 236–240.
5. Yoojeong Noh, Choi K. K., Liu Du Selection of Copula to Generate Input Joint CDF for RBDO // ASME 2008 Interna-tional Design Engineering Technical Conferences and Comput-ers and Information in Engineering Conference. – August 3–6, 2008. – Vol. 1. – P. 1145–1156. DETC2008-49494.
6. Bellman R. E. Adaptive Control Processes: a Guided Tour // Princeton University Press, 1961. – 255 pp.
7. Rogers J. L., Nicewander W.A. Thirteen Ways to Look at the Correlation Coefficient // The American Statistician. – 1988. – Vol. 42, № 1. – P. 59–66.
8. Fieller E. C., Hartley H. O., Pearson E. S. Tests for Rank Correlation Coefficients // Biometrika. – 1957. – Vol. 44, № 3/4. – P. 470–481.
9. Kendall M. A New Measure of Rank Correlation // Bio-metrika. – 1938. – Vol. 30, № 1/2. – P. 81–89.
10. Shapiro S. S., Wilk M. B. An Analysis of Variance Test for Normality // Biometrika. – 1965. – Vol. 52, № 3. – P. 591–611.
11. Sklar A., Fonctions de répartition à n dimensions et leurs marges // Paris Publications de l'Institut de Statistique de l'Université de Paris. – 1959. – Vol. 8. – P. 229–231.
12. Fantaccini D. Modelirovanie mnogomernyh raspre-deleniy s ispol'zovaniem kopula-funkciy. Chast' I // Pri-kladnaya ekonometrika. – 2011. – T. 2, № 22. – S. 98–134.
13. Penikas G. I., Simakova V. B. Upravlenie procentnym riskom na osnove kopuly-GARCH modeley // Prikladnaya ekonometrika. – 2009. – T. 1, № 13. – S. 3–36.
14. Karakas M. A. Modelling Temperature Measurement Data by Using Copula Functions // Bitlis Eren University Journal of Science and Technology. – 2017. – Vol. 7, № 1. – P. 27–32.
15. Bezak N., Zabret K., Šraj M. Application of Copula Func-tions for Rainfall Interception Modeling // Water. – 2018. – Vol. 10, № 8. 995
16. Zhang Y., Beer M., Quek S.T. Long-Term Performance As-sessment and Design of Offshore Structure // Computers and Structures. – 2015. – Vol. 154. – P. 101–115.
17. Yang S. C., Liu T. J., Hong H. P. Reliability of Tower and Tower-Line Systems Under Spatiotemporally Varying Wind or Earthquake Loads // Journal of Structural Engineering. –2017. – Vol. 143, № 10: 04017137.
18. Kartashevskiy I. V. Ispol'zovanie kopul v statistiche-skom analize telekommunikacionnogo trafika // Info-kommunikacionnye tehnologii. – 2016. – T. 14, № 4. – S. 405–412.
19. Akaike H. A New Look at the Statistical Model Identifi-cation // IEEE Transactions on Automatic Control. – 1974. – Vol. 19, № 6. – P. 716–723.
20. Schwarz G. Estimating the dimension of a model // An-nals of Statistics. – 1978. – Vol. 6, № 2. – P. 461–464.
21. Epanechnikov V.A. Neparametricheskaya ocenka mnogo-mernoy plotnosti veroyatnosti // Teoriya veroyatnostey i ee primeneniya. – 1969. – T. 14, № 1. – S. 156–161.
22. Sheather S.J., Jones M.C. A Reliable Data-Based Band-width Selection Method for Kernel Density Estimation // Journal of the Royal Statistical Society. Series B. – 1991. – Vol. 53, № 3. – P. 683–690.
