Приведены результаты анализа формы зерен портландцемента, подвергшегося обработке в мельнице вихревого типа. Для оценки формы цементных частиц предложен безразмерный критерий, представляющий собой возведенное в степень отношение площади частицы к квадрату длины её периметра. С использованием предложенного критерия подтверждена научная гипотеза о повышении активности цемента за счет модификации формы частиц цемента, обработанного в мельнице вихревого типа, заключающаяся в придании частицам более округлой формы. Для оценки формы частиц установ-лена область рациональных целочисленных значений порядка предложенного критерия.
активация, мельница вихревого типа, критерий формы частиц, рельефность частиц, свойства портландцемента
Для объяснения повышения прочности цементно-песчаных образцов на активированном в мельнице вихревого типа цементе, изготовленных из равноподвижных растворных смесей при пониженном водоцементном отношении, была выдвинута научная гипотеза о модификации зерен цемента от угловой к более окатанной форме, что и объясняло отмеченные особенности активированного в мельнице вихревого типа цемента [1], требующая, однако, теоретического и экспериментального обоснования.
Проблема оценки формы разнообразных геометрических фигур актуальна для различных отраслей науки и промышленности, в частности, в фармацевтической, химической, горнодобывающей и строительной отраслях [2-5]. В строительной индустрии такая задача возникает, например, при исследовании прочности и жесткости конструкций, находящихся под воздействием статических и динамических нагрузок [6], или влияния формы частиц на плотность их упаковки, а, следовательно, на расход цемента при подборе составов растворов и бетонов [7].
Наиболее распространенным способом оценки формы частиц является метод визуализации, который основывается на рассмотрении двумерной проекции профиля частицы. В настоящее время разработаны различные автоматизированные системы визуализации и анализа изображений, обеспечивающие получение информации не только о размере, но и о форме частиц [8-13]. Для таких целей используются различные параметры, позволяющие сделать возможным как сам анализ, так и выполнить статистическую обработку результатов измерений. Чаще всего для описания формы используются такие параметры, как выпуклость, округлость, удлинение, абсолютная и относительная величина удлинения и др. [14-18]. Достоинством использования таких параметров является их достаточная простота, но данные параметры не дают возможности оценить наряду с формой частицы такую ее важную характеристику, как шероховатость или рельефность поверхности частицы.
В то же время ряд предложенных критериев для оценки формы частицы имеют ограничения по их применению. В качестве такого примера приведем аналитическую оценку геометрической формы частиц по коэффициенту формы плоской области (рис.1), предложенного В.И. Коробко и являющегося количественной характеристикой формы области, выражаемой через контурный интеграл [19, 20]:
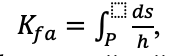(1)
где ds – линейный элемент контура области (рисунок 1); h – высота, опущенная из полюса, взятого внутри области, на касательную к переменной точке контура; P – периметр области.
Для контура, составленного из криволинейных и прямолинейных участков, значение коэффициента формы области вычисляется по формуле:
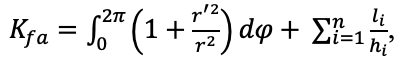(2)
где r = r (φ) – полярный радиус контура области с полюсом в точке «а» (рис. 1 а), li, hi – соответственно длина i-ой стороны многоугольника и опущенная из полюса O на i-ю сторону высота (рис. 1 б).
Вычисление для фигур произвольного очертания, далеких от классически форм, ввиду сложности формулы (2) становится затруднительным, а при наличии вогнутостей определение коэффициента формы
теряет смысл, так как в этом случае невозможно опустить перпендикуляр из полюса непосредственно на периметр рассматриваемой области (сторона 34 на рис. 1 в).
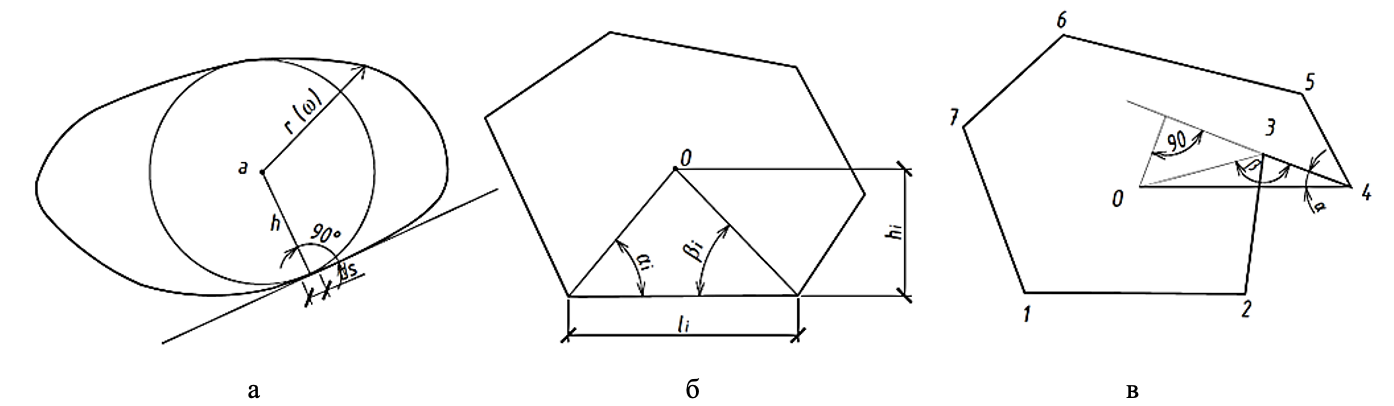
Рисунок 1. Схемы к вычислению коэффициента формы по В.И. Коробко [20]
а – область с криволинейным контуром; б – область (выпуклая) с полигональным контуром;
в – область (вогнутая) с полигональным контуром
В связи с вышеизложенным, для оценки формы произвольных плоских геометрических фигур предлагается безразмерный критерий ki, представляющий собой отношение площади фигуры к квадрату длины ее периметра в степени i:
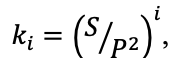(3)
где S – площадь фигуры произвольной формы, P – длина ее периметра.
В формуле (3) степень i, являющаяся порядком критерия ki, принимающая как дробные, так и целочисленные значения: i = 1/n, …, 1, …, n, где n – число натурального ряда.
Рассмотрим применение критерия в модельной задаче по оценке близости формы ряда геометрических фигур в виде многоугольников к форме круга, принятого в качестве эталона. Результаты вычислений критерия
для плоских фигур правильной формы приведены в таблице 1 при значениях n = 1, 2, 4, 8.
Из таблицы 1 следует, что для каждого порядка i в предложенном критерии оценки формы плоских фигур (3) для круга величина имеет наибольшее значение, к которому приближается величина этого критерия для правильных многоугольников с ростом числа их сторон. Кроме того, известно, что из всех n-угольников равной площади, правильный многоугольник имеет наименьший периметр. Поэтому любой неправильный n-угольник будет иметь меньшее значение ki, чем правильный. Таким образом, представляется возможным использование предложенного критерия (3) для сравнения различных геометрических фигур, в том числе как выпуклых, так и вогнутых.
Таблица 1 – Значения критерия для ряда геометрических фигур
|
Порядок критерия
Вид плоской фигуры |
k1/8 |
k1/4 |
k1/2 |
k110-1 |
k210-2 |
k410-4 |
k810-9 |
|
Круг |
0,729 |
0,531 |
0,282 |
0,796 |
0,633 |
0,401 |
1,62 |
|
Квадрат |
0,707 |
0,500 |
0,250 |
0,625 |
0,390 |
0,152 |
0,23 |
|
Пятиугольник |
0,716 |
0,512 |
0,262 |
0,688 |
0,473 |
0,224 |
0,50 |
|
Шестиугольник |
0,720 |
0,518 |
0,269 |
0,722 |
0,521 |
0,271 |
0,74 |
|
Восьмиугольник |
0,724 |
0,524 |
0,275 |
0,754 |
0,569 |
0,323 |
1,05 |
В таблице 2 приведена оценка отличия сравниваемых фигур, выполненная для критерия формы ki по формуле:
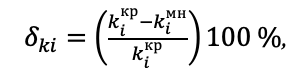(4)
Из таблицы 2 следует, что независимо от порядка критерия ki наибольшее отличие формы многоугольника от круга наблюдается для квадрата, наименьшее – для восьмиугольника, что подтверждает вышесказанное относительно снижения отличия формы круга от формы многоугольника с ростом числа его сторон. При этом с ростом по абсолютной величине порядка i растет чувствительность предложенного критерия для оценки формы частиц, например, при сравнения фигур «круг – восьмиугольник» чувствительность оценки отличия восьмиугольника от круга растет с 0,67 % (при i = 1/8) и 5,2 % (при i = 1) до 35,19 % (при i = 8), т.е. при порядке i = 8 по формуле достигается более высокая достоверность отличия рассматриваемых фигур.
В дополнение к оценке формы частиц критерий (3) был использован для установления другой такой важной их характеристики, как рельефность. С этой целью были рассмотрены модельные частицы определенной формы (круг, эллипс, прямоугольник) с разной степенью рельефности поверхности (рисунок 2), для которых была вычислена величина критерия (3) при значениях n = 1, 2, 4, 8 (таблица 3).
Таблица 2 – Оценка отличия многоугольников от формы круга
|
Отличие критериев Сравниваемые виды плоских фигур |
|
|
|
|
|
|
|
|
Круг/квадрат |
2,97 |
5,86 |
11,38 |
21,46 |
38,31 |
61,94 |
85,80 |
|
Круг/пятиугольник |
1,80 |
3,57 |
7,00 |
13,52 |
25,21 |
44,06 |
69,14 |
|
Круг/шестиугольник |
1,21 |
2,41 |
4,76 |
9,28 |
17,71 |
32,28 |
54,32 |
|
Круг/восьмиугольник |
0,67 |
1,33 |
2,64 |
5,20 |
10,14 |
19,25 |
35,19 |
Из таблицы 3 следует, что для частиц определенного вида с увеличением их шероховатости поверхности при фиксированном порядке i величина критерия (3) снижается, причем с возрастанием порядка i различие между рельефностью фигур вида 1 и рельефностью фигур вида 4 становится более существенным.
Можно заметить, что значения критерия формы ki для разного вида фигур различной степени рельефности близки друг к другу. Например, для круга при рельефности типа 3 – k1/8 = 0,671, а для прямоугольника рельефности типа 1 – k1/8 = 0,696, что может вызвать сомнение в возможности применения критерия (3).
Поэтому необходимо выполнять оценку степени рельефности частиц одного или близкого вида, для чего анализируемые частицы предварительно ранжируется по виду на группы и уже в каждой группе выполняется их анализ по степени рельефности.
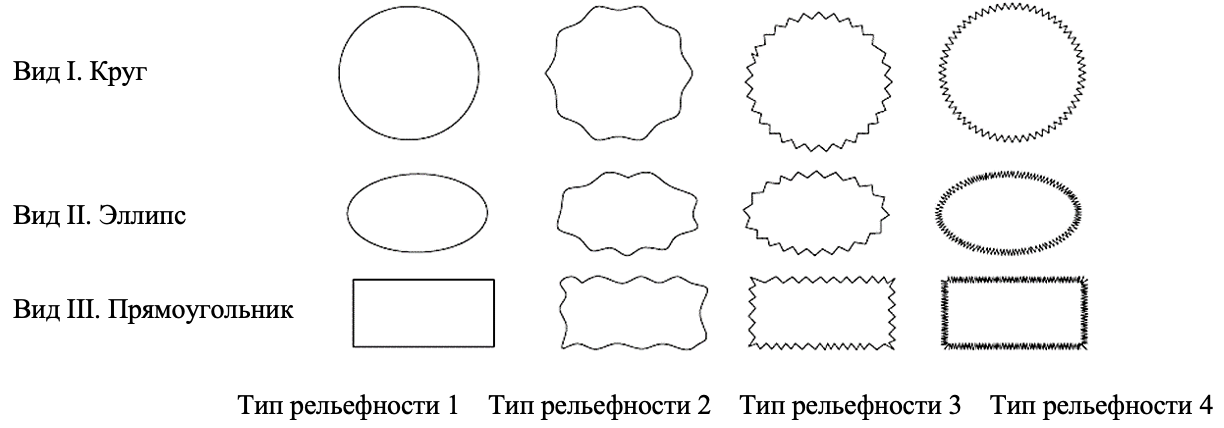Рисунок 2. Виды плоских фигур с различными типами рельефности (I – круг, II – эллипс, III - прямоугольник)
Таблица 3 – Значение критерия ki для фигур различного вида и типа рельефности
|
Порядок критерия Вид фигуры и тип ее рельефности |
k1/8 |
k1/4 |
k1/2 |
k110-1 |
k210-2 |
k410-4 |
k810-9 |
|
Вид I. Круг – Тип рельефности 1 |
0,728 |
0,531 |
0,282 |
0,79 |
0,6332 |
0,40101 |
1,61 |
|
Вид I. Круг – Тип рельефности 2 |
0,718 |
0,515 |
0,266 |
0,70 |
0,5013 |
0,25130 |
0,63 |
|
Вид I. Круг – Тип рельефности 3 |
0,671 |
0,450 |
0,202 |
0,41 |
0,1689 |
0,02855 |
0,0082 |
|
Вид I. Круг – Тип рельефности 4 |
0,601 |
0,361 |
0,130 |
0,17 |
0,0291 |
0,00085 |
0,0000073 |
|
Вид II. Эллипс – Тип рельефности 1 |
0,719 |
0,517 |
0,267 |
0,71 |
0,5142 |
0,26439 |
0,70 |
|
Вид II. Эллипс – Тип рельефности 2 |
0,705 |
0,497 |
0,247 |
0,61 |
0,3758 |
0,14126 |
0,20 |
|
Вид II. Эллипс – Тип рельефности 3 |
0,672 |
0,452 |
0,205 |
0,42 |
0,1766 |
0,03121 |
0,010 |
|
Вид II. Эллипс – Тип рельефности 4 |
0,500 |
0,250 |
0,062 |
0,03 |
0,0015 |
0,000002 |
5х10-11 |
|
Вид III. Прямоугольник – Тип рельефности 1 |
0,696 |
0,485 |
0,235 |
0,55 |
0,3086 |
0,09525 |
0,09 |
|
Вид III. Прямоугольник – Тип рельефности 2 |
0,686 |
0,471 |
0,222 |
0,49 |
0,2458 |
0,06043 |
0,04 |
|
Вид III. Прямоугольник – Тип рельефности 3 |
0,628 |
0,394 |
0,155 |
0,243 |
0,0590 |
0,00348 |
0,00012 |
|
Вид III. Прямоугольник – Тип рельефности 4 |
0,445 |
0,198 |
0,039 |
0,015 |
0,0002 |
0,000001 |
310-14 |
Анализируя результаты, приведенные в таблицах 2 и 3, необходимо отметить, что с ростом порядка i критерий становится более чувствительным к изменению формы частиц и степени рельефности их поверхности, а, значит, для более тонкого анализа фигур, мало отличающихся по форме, целесообразно использовать критерий более высокого порядка – не ниже i = 4.
Кроме установленного факта увеличения при обработке в мельнице вихревого типа дисперсности цемента (см. таблицу 4 в [1]) в качестве научной гипотезы повышения активности обработанного в мельнице вихревого типа цемента можно предположить, что в процессе его вихревой обработки, по аналогии с барханными песками, происходит изменение формы частиц цемента от угловатой к более округлой. Такое изменение формы частиц может приводить к существенным изменениям в свойствах цементных систем, полученных на модифицированном в вихревой мельнице портландцементе (см. таблицы 5-8 в [1]). Подтверждение выдвинутой научной гипотезы о преобразовании формы частиц цемента в процессе их обработки в мельнице вихревого типа от угловатой к более окатанной устанавливали с использованием предложенного критерия ki.
Материалы и методы исследования. Для анализа формы цементных зерен до и после обработки в мельнице вихревого типа были отобраны три пробы цемента [1]: проба №1 – исходный цемент (контрольный); проба №2 – тот же цемент, активированный в вихревой мельнице с классификационной диафрагмой диаметром d90 мм; проба №3 – то же, с классификационной диафрагмой диаметром d102 мм. Диаметр диафрагмы влияет на степень измельчения цемента – чем его значение меньше, тем дисперсность получаемого цемента выше.
Как было показано выше, наибольшее значение критерий формы принимает для шарообразной частицы, имеющей сечения в виде круга. При этом значение критерия формы зависит от его порядка i, уменьшаясь по величине с его ростом (см. таблицу 1), но не зависит от размера шарообразной частицы. Поэтому в качестве эталона сравнения для активированных в вихревой мельнице частиц цемента была принята величина критерия формы для круга как идеальной «по степени округлости» фигуры. Таким образом, чем ближе будет величина расчетного значения коэффициента
частицы к принятому ее эталонному значению, тем более округлую форму будет иметь анализируемая частица, а применение статистической обработки позволяет установить статистическую значимость такого различия.
Результаты исследования. Для проведения сравнительного анализа в части преобразования формы частиц цемента после обработки в мельнице вихревого типа случайным образом выбиралось по пятьдесят частиц из каждой пробы цемента (рис. 3), для которых были вычислены необходимые геометрические параметры и рассчитаны значения критерия формы различного порядка, приведенные в таблице 4.
Рисунок 3. Исследуемые пробы цемента
а) проба №1 – контрольный цемент; б) проба №2 – тот же цемент, активированный в вихревой мельнице с классификационной диафрагмой диаметром d90 мм; в) проба №3 – то же, с классификационной диафрагмой диаметром d102 мм
Таблица 4 – Средние значения критерия формы для проб цемента
|
Порядок критерия Номер пробы |
k1/8 |
k1/4 |
k1/2 |
k110-1 |
k210-2 |
k410-4 |
k810-9 |
|
№1 |
0,706 |
0,498 |
0,248 |
0,618 |
0,386 |
0,155 |
0,280 |
|
№2 |
0,713 |
0,508 |
0,258 |
0,668 |
0,448 |
0,203 |
0,440 |
|
№3 |
0,712 |
0,507 |
0,257 |
0,662 |
0,439 |
0,195 |
0,390 |
Как видно из таблиц 1 и 4, значения критерия формы частиц активированного цемента (пробы №2 и №3), не зависимо от порядка i, имеют бóльшие значения, чем неактивированного (проба №1), что подтверждает предположение об их более округлой (окатанной) форме. Причем, если с уменьшением порядка i различие значений коэффициента формы частиц для эталона (круга) и цементных частиц может составлять всего (2-3) % (при i = 1/8), то при его значении i = 8 такое различие достигает уже 80-90 %, т.е. с ростом порядка предложенный критерий становится более чувствительным к изменению формы частиц.
Заключение и выводы. Использование предложенного критерия формы частиц (3) позволяет сделать вывод о том, что в процессе активации цемента в мельнице вихревого типа происходит модификация цементных частиц, заключающаяся в получении частиц более округлой формы после их вихревой обработки.
С целью определения значимости преобразования формы частиц цемента, подвергшегося обработке в мельнице вихревого типа, была выполнена статистическая обработка полученных данных с применением t-критерия Стьюдента [21], которая подтвердила выдвинутую гипотезу.
Таким образом, проанализировав полученные данные можно сделать следующие выводы:
а) предложен критерий для оценки формы частиц, представляющий собой отношение площади частицы к квадрату длины её периметра, возведенное в степень i, являющейся порядком критерия;
б) для оценки формы частиц установлено рациональное целочисленное значение порядка критерия i, которое рекомендуется принимать не ниже 4;
в) с использованием предложенного критерия подтверждена научная гипотеза о повышении активности цемента, подвергшегося обработке в мельнице вихревого типа, за счет модификации формы частиц цемента от угловатой к более округлой.
1. Кондращенко, В.И. Активация цемента в мельнице вихревого типа. Часть 1. Свойства активированного в вихре-вой мельнице цемента / В.И. Кондращенко, С.П. Титов // Техника и технология силикатов. – 2019. – №4. – С. 115-119.
2. Альмяшева, О.В. Размер, морфология и структура частиц нанопорошка диоксида циркония, полученного в гидротермальных условиях / О.В. Альмяшева и др. // Нано-системы: физика, химия, математика. – 2010. – №1. – С. 26-36.
3. Андриевский, Р.А. Порошковое материаловедение / Р.А. Андриевский. – М.: Металлургия, 1991. 205 с.
4. Зозуля, П.В. Оптимизация гранулометрического состава и свойств заполнителей и наполнителей для сухих строительных смесей // Сб. тезисов докладов 3-й Междуна-родной конференции BaltiMix. – СПб. 2003. С. 12-13.
5. Rodriguez, J.M. Particle Shape Determination by Two-Dimensional Image Analysis in Geotechnical Engineer-ing / J.M. Rodriguez, J. Johansson, T. Edeskär // Nordic Ge-otechnical Meeting – 2012, Copenhagen, Denmark, pp. 355-363.
6. Дебердеев, Т.Р. Прочность тяжелого бетона на портландцементе, обработанном в аппарате вихревого слоя / Т.Р. Дебердеев, Р.А. Ибрагимов, Е.В. Королев, В.В. Лексин // Строительные материалы. – 2017. – №10. – С. 28-31.
7. Попов, Л.Н. Структурообразование в системах при производстве строительных материалов / Л.Н. Попов, И.Б. Аликина, Б.А. Усов. – НИЦ ИНФРА-М, 2018. 61 с.
8. Бикмухаметов, А.Р. Активированные щелочами цементы на основе мергеля с добавкой известняка / А.Р. Бикмухаметов, Р.З. Рахимов, Н.Р. Рахимова, Л.И. Потапова // Техника и технология силикатов. – 2019. – №2(26). – С. 5-6.
9. Высокоэффективные технологии измерения формы и размера частиц при разработке и обеспечении качества твердых лекарственных форм. Фармацевтическая отрасль – 2013. – № 3(38). – С. 96-100.
10. Новик, Е.С. Методы оценки формы частиц в фарма-цевтической отрасли / Е.С. Новик, А.В. Доренская, Н.А. Бо-рисова, О.В. Гунар // Фармация. – 2017. №4: С. 3-6.
11. Новик, Е.С. Оценка размера и формы частиц фар-мацевтических субстанций микроскопическим методом / Е.С. Новик [и др.] // Успехи современного естествознания. – 2016. – № 11. – С. 249-255.
12. Кошкарев, С.А. К оценке фактора формы частиц с использованием комплексного дисперсионного анализа для снижения проскока пыли выбросов в пылеулавливающих устройствах аспирации стройиндустрии / С.А. Кошкарев и др. // Инженерный вестник Дона. – 2018. – №4(51). – С. 244.
13. Игнатова А.М. Методология оценки морфометри-ческих параметров частиц аэродисперсных систем калий-ных солей / А.М. Игнатова, М.Н. Игнатов // Материалы I Международной научно-практической конференции «Акту-альные проблемы охраны труда и безопасности производ-ства, добычи и использования калийно-магниевых солей (Пермь, 14 – 15 мая 2018 г.). Пермский национальный ис-следовательский политехнический университет. – 2018. – С. – 453-464.
14. Беленко, О.А. Оценка формы частиц и дисперсного состава грубодисперсных фракций атмосферных аэрозолей / О.А. Беленко, К.П. Куценогий // ГЕО-СИБИРЬ. – 2007. – №3. – С. 339-343.
15. Емшанова, С.В. Влияние формы и размера частиц субстанций на качество готовых лекарственных средств / С.В. Емшанова, Р.А. Абрамович, О.Г. Потанина // Научно-производственный журнал. – 2014. – №2 (7). – С. 50-63.
16. Злобин, И.А. Влияние способов механического воздействия на геометрическую форму и характер поверх-ности частиц цемента / И.А. Злобин, О.С. Мандрикова, И.Н. Борисов // Цемент и его применение. – 2015. – №5. – С. 56-60.
17. Неумержицкая, Н.В. Оценка фракционного состава, формы частиц и концентрации древесной пыли в атмосфер-ном воздухе / Н.В. Неумержицкая // Инженерный вестник Дона. – 2018. – №1(48). – С. 140.
18. Панигархи, П.К. Морфология цементных частиц после помола в различных агрегатах и ее влияние на свой-ства цемента / П.К. Панигархи и др. // Цемент и его приме-нение. – 2010. – №1. – С. 114-122.
19. Фетисова, М. А., Володин С. С. Коэффициент фор-мы как геометрическая характеристика // Молодой ученый. 2011. №5. Т.1. С. 105-107.
20. Коробко, А.В. Геометрическое моделирование формы области в двумерных задачах теории упругости / А.В. Коробко. – М.: Изд-во АСВ, 1999. – 320 с.
21. Кобзарь, А.И. Прикладная математическая стати-стика. Для инженеров и научных работников. М.: Физмат-лит, 2006. – 816 с.
